2017년 IEEE TMI에 발표된 논문으로, Physics/Model based unrolling iterative deep learning methods 중 하나이다.
딥러닝을 이용한 MR Reconstruction method 중 하나인 unrolling iterative method에 대해 간단히 설명하자면, 모델 구조에 MR physics를 사용한 것이라고 보면 된다.
이미지 자체만을 이용해 딥러닝 모델을 학습시키는 end-to-end method와 달리, unrolling iterative method는 Compressed Sensing의 idea를 적용한다. Learning proces와 problem solving algorithm이 번갈아가며 iterative하게 진행된다.
CascadeNet은 이러한 unrolling iterative method 중 초기 모델로, 이후 이 모델을 base로 한 다른 논문이 많이 나왔다.
IEEE Xplore Full-Text PDF:
ieeexplore.ieee.org
Official Code (PyTorch)
GitHub - js3611/Deep-MRI-Reconstruction: Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction: Implementati
Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction: Implementation & Demo - GitHub - js3611/Deep-MRI-Reconstruction: Deep Cascade of Convolutional Neural Networks for MR ...
github.com
Problem Formulation
full-sampled image $ x \in \mathbb{C}^N $ (Label)와 undersampled k-space $ y = F_ux + e \in \mathbb{C}^M $ (Input)에 대해 다음과 같이 optimization problem을 정의할 수 있다. ($e$는 noise)
$min_x ||x-f_{cnn}(x_u|\theta)||^2_2 + \lambda||F_ux-y||^2_2$
이 때 $ x_u = F_u^Hy $로, $y$의 빈 부분을 0으로 채운 zero-filled reconstruction이며,
$F_u = MF$은 undersampling mask $M$과 2D DFT $F$를 이용한 undersampled Fourier encoding matrix이다.
위 식은 두 개의 부분으로 나누어 볼 수 있다.
1. $min_x ||x-f_{cnn}(x_u|\theta)||^2_2$ : CNN
- CNN을 통해 zero-filled reconstruction $x_u$를 full-sampled image $x$로 reconstruction하는 과정이다.
- $\theta$는 CNN parameter이다.
- 두 image 간의 L2 loss를 최소화하는 방향으로 학습이 진행된다.
2. $\lambda||F_ux-y||^2_2$ : Data Consistency Layer
- Reconstructed image와 $y$와의 data consistency를 보장하기 위한 부분이다.
- 우리는 $y$에 해당하는, already-known k-space 값들을 보존할 필요가 있다. (이미 알고 있는 정보이기 때문에 최대한 변형하지 않도록)
- 따라서 Reconstructed image $x$을 k-space로 변환(Fourier transform)한 후, undersampling을 적용한 값과 $y$의 차이를 최소화하도록 한다.
Network Architecture

- CascadeNet의 구조이다. CNN Block과 DC(Data Consistency) Block이 번갈아 가며 reconstruction이 진행된다.
- CNN과 DC layer을 $n_c$회 반복하며, 학습은 end-to-end로 이루어진다.
- Input은 image domain의 zero-filled reconstruction이며,
- Label은 image domain의 fully-sampled image이다.
- Input shape는 $\mathbb{R}^{2N_xN_y}$로, complex image의 실수부와 허수부를 concat하여 사용한다.
CNN Block
- 이미지의 missing point를 재구성하는 역할을 한다.
- 단순한 Convolution network 구조이다.
- $n_d - 1$개의 2D Convolution layer $C_i$와, final layer $C_{rec}$으로 이루어져 있다.
- 각 $C_i$는 kernel size $k=3$을 이용하며, filter 개수는 $n_f=64$를 사용하였다. Activation function으로는 ReLU를 사용하였다.
- 마지막 layer $C_{rec}$의 kernel size는 $k=3$로 동일하며, image domain으로 돌아가기 위해 $n_f=2$을 사용했다.
- 마지막으로 Residual connection을 사용했다. input과 마지막 $C_{rec}$을 더해 최종 output을 출력한다.
DC Block
- Already-known k-space data의 보존을 위한 block이다. (Data consistency)
- Learning process가 아니며, 따라서 trainable parameter도 없다.
- sampling mask $\Omega$에 대해, 각 point에 대해 다음과 같이 처리한다.
$s_{rec}(j)=s_{cnn}(j)$ if $j \notin \Omega$
$=\frac{s_{cnn}(j)+\lambda s_0(j)}{1+\lambda}$ if $j \in \Omega$
* $s_{cnn} = Fx_{cnn} = Ff_{cnn}(x_u|\theta)$ : CNN으로 reconstruct한 image의 k-space image
* $s_0 = Fx_u= FF^H_uy$ : zero-filled reconstruction의 k-space image
- 즉, k-space 값이 sampling mask에 포함되지 않은 경우 (unknown), CNN으로 얻은 값을 그대로 사용한다.
- k-space 값이 sampling mask에 포함된 경우 (already-known), CNN으로 얻은 값과, 원래의 zero-filled reconstruction 값(original value)을 linear combination 하여 사용한다.
- Already-known point의 값을 그대로 사용하지 않는 이유는, inherent noise 때문이다.
- $\lambda \rightarrow$ ∞으로 놓으면, already-known point의 값을 그대로 사용할 수 있다. (Noiseless case)
- 위의 식을 다음과 같이 하나로 표현할 수 있다.
$f_{dc} (s, s_0;\lambda) = \Lambda s + \frac{\lambda}{1+\lambda}s_0$
* where $\Lambda_{kk} = 1$ if $j\notin\Omega$,
$= \frac{1}{1+\lambda}$ if $j \in\Omega$
- 여기에, 마지막으로 다시 image domain으로 되돌아가는 과정까지 포함하면 식은 다음과 같다.
$f_L(x,y;\lambda)=F^H\Lambda Fx+\frac{\lambda}{1+\lambda}F_u^Hy$
Experiments
Dataset
- 10명의 fully sampled cardiac cine MR scan을 이용했다.
- 각 scan은 30개의 slice를 포함하고 있어, 총 300개의 2D image를 얻을 수 있었음.
- 각 data는 32-channel로, sampling matrix size는 192*190, zero-filled matrix size는 256*256
- Data augmentation으로는 vertical/horizontal shift, [0, 2pi)의 rotation, horizontal flip, elastic deformation을 사용하였음.
Effect of DC Layer
$Dn_d-Cn_c$로 각 모델의 구조를 표현하였다. $n_d$는 CNN의 convolution layer의 개수, $n_c$는 반복되는 CNN-DC Block의 개수를 의미한다.
- 깊이가 같지만 DC Block의 개수가 다른 두 개의 모델 $D5-C2$, $D11-C1$의 성능을 비교하였다.
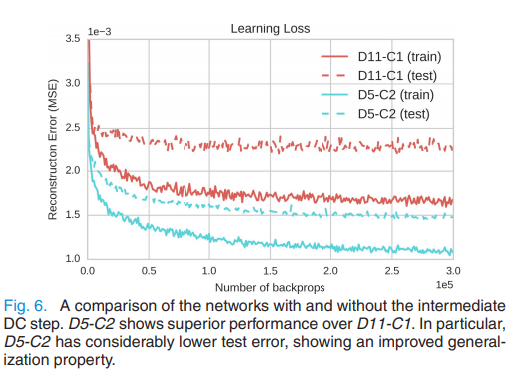
- $D5-C2$가 더 나은 성능과 더 높은 generalization property(일반화 성능)을 보였다.
- 이는 DC Block이 overfitting을 방지하는 데에 도움이 됨을 의미한다.
Effect of cascading iterations $n_c$
- Convolution layer의 개수 $n_d$를 고정하고, iteration 수를 달리하여 실험했다. ($n_c \in \{1, 2, 3, 4, 5\}$)
- Greedy approach를 사용했다. 작은 $n_c$부터 훈련해서, $n_c=k-1$인 모델의 weight을 이용해 $n_c=k$의 weight을 초기화시켰다. (Weight transfer)
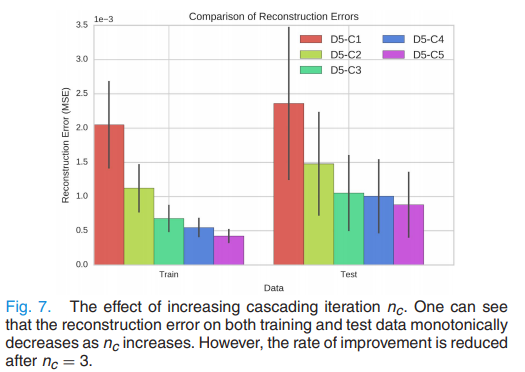
- 모델의 깊이가 깊어질수록 overfitting의 정도가 심해지는 경향이 있었으나, Test error은 항상 감소했다.
- 그러나 성능의 증가폭은 $n_c=3$부터 점차 감소했으며, 모델의 깊이가 깊어질수록 error의 편차 역시 감소했다.
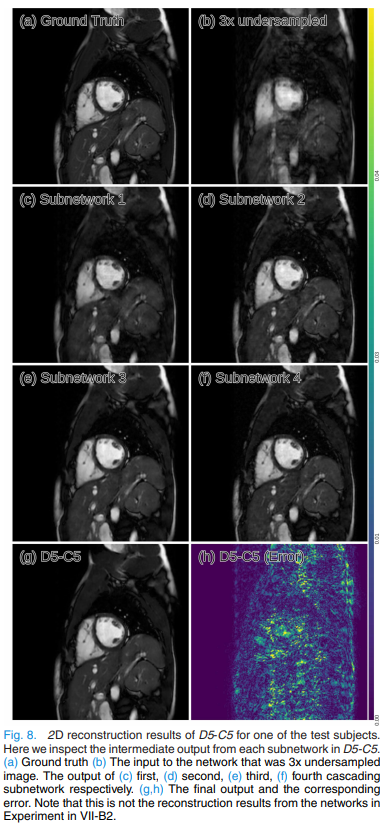
- 위 Figure은 $D5-C5$에서 각 block에서의 interemediate result를 나타낸 것인데, inference가 진행될수록 점차적으로 output image를 reconstruction하고 선명해지는 것을 확인할 수 있다.
Unrolling iterative MR reconstruction method 중 하나인 CascadeNet 논문이다.
초기 모델이라 그런지 실험과 분석, 구조가 간단하고,
PyTorch로 구현된 코드도 공개되어 있어 Unrolling iterative method에 대해 이해하기 좋다.