[딥러닝 논문리뷰 + 코드] Uncertainty-Driven Loss for Single Image Super-Resolution (NeurIPS 2021)

NeurIPS 2021에서 발표된 논문으로, single image super-resolution (SISR)을 위해 uncertainty를 이용한 loss를 제안했다. 맨 아래에 PyTorch로 구현된 코드를 정리해 놓았다.

 

논문 링크: https://papers.nips.cc/paper/2021/file/88a199611ac2b85bd3f76e8ee7e55650-Paper.pdf

Supplementary: https://papers.nips.cc/paper/2021/file/88a199611ac2b85bd3f76e8ee7e55650-Supplemental.pdf

Homepage: https://see.xidian.edu.cn/faculty/wsdong/Projects/UDL-SR.htm

https://see.xidian.edu.cn/faculty/wsdong/Projects/UDL-SR.htm

 

1. Introduction

Single image super-resolution (SISR)은 low-resolution (LR) 이미지를 high-resolution (HR) 이미지로 변환하는 문제이다. SRCNN을 시작으로 하여 EDSR, DPDNN, RCAN, SAN, MoG-DUN 등 다양한 딥러닝 모델들이 개발되어 왔다.

 

 

SISR에서는 보통 MSE나 L1 loss 같은, pixel-wise difference를 이용한 loss가 주로 이용된다. 이러한 loss 함수들은 모든 pixel에 대한 중요도를 같게 주는데, SISR과 같은 low-level vision task에서는 texture이나 edge 같은 부분이 더 많은 정보를 담고 있기 때문에, 이러한 부분에 더 많은 weight를 주어야 한다.

 

Texture나 edge 등, 중요한 visual information을 담고 있는 부분은 보통 high uncertainty를 갖는다. 본 논문에서는 uncertainty estimation을 통해 각 pixel의 uncertainty를 측정하고, 기존의 uncertainty loss들과 다르게 uncertainty가 높은 부분의 weight를 더 주는 방식의 새로운 uncertainty-driven loss (UDL)을 제안한다.

 

 

2. Related work

일반적으로 딥러닝 모델에서의 uncertainty loss는 다음과 같은 형태를 띈다.

 

$\mathcal{L}=\frac1N\sum_{i=1}^N\frac{||x_i-f(y_i)||_2}{2\sigma^2_i}+\frac12\ln\sigma^2_i$

 

이 때 $f(y_i)$는 learned mean, $\sigma^2_i$는 variance를 나타낸다. 이러한 형태의 loss function은 noisy data에 대한 robustness를 증가시키는 역할을 한다. 일반적으로 high uncertainty를 가진 pixel은 그 값이 unreliable하다는 뜻이기 때문에 해당하는 loss값을 attenuation(감쇠)하는 것이다.

 

이 때 numerical stability를 위해 다음과 같이 log variance $s_i:=\log\hat\sigma^2_i$를 예측하게 한다.

 

$\mathcal{L}_{EU}=\frac1N\sum_{i=1}^N\exp(-s_i)||x_i-f(y_i)||_1+s_i$

 

반면 SISR task의 경우 high uncertainty를 가진 pixel 들은 복잡한 texture 혹은 edge 부분을 나타내는 것이므로, 일반적인 경우와 반대로 더 큰 weight를 주어야 한다. 따라서 SISR task에 위와 같은 loss를 사용하면 오히려 성능이 하락하게 된다.

 

 

 

3. Methodology

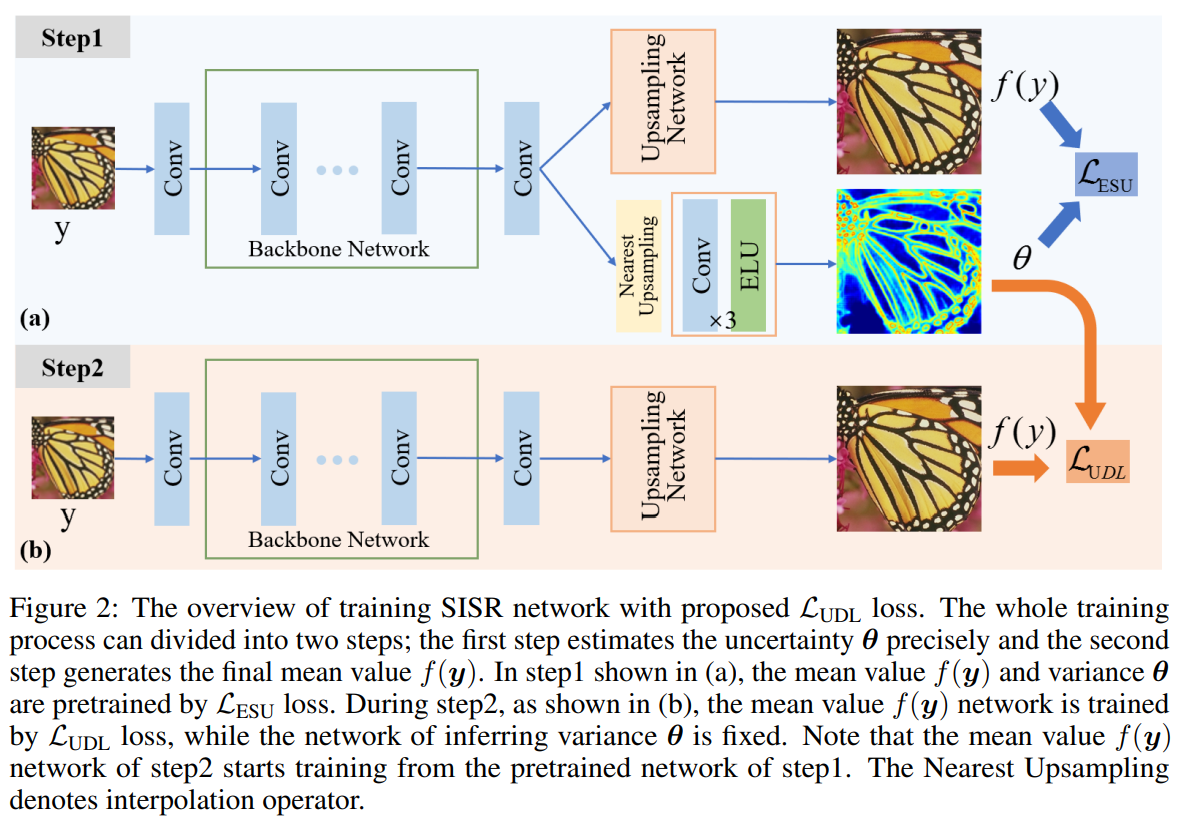
본 논문에서는 two-step 으로 모델의 훈련을 진행한다.

 

1) Estimating uncertainty (EU)

 

이 단계에서는 기존의 uncertainty 측정법에 Jeffrey's Prior을 결합하여 보다 sparse하게 uncertainty를 측정할 수 있는 방법을 제안한다. (과정 생략) 이 때 사용하는 loss의 형태는 다음과 같다.

 

$\mathcal{L}_{ESU}=\frac1N\sum_{i=1}^N\exp(-s_i)||x_i-f(y_i)||_1+2s_i$

 

여기서 $x_i$, $y_i$는 각각 HR과 LR 이미지를 나타내고, $s_i$는 estimated log variance를 의미한다. 이 loss를 이용해 SISR task를 수행하면 결과 이미지와 uncertainty map을 얻을 수 있는데, 이는 다음과 같다.

 

 

2) Uncertainty-Driven Loss

 

기존의 uncertainty 측정법 ($\mathcal{L}_{EU}$)보다 본 논문에서 새롭게 제안한 방법 ($\mathcal{L}_{ESU}$)가 더 sparse한 uncertainty map을 얻을 수 있음을 확인할 수 있다. 단, 위에서 언급한 바와 같이 이 경우 SISR의 성능은 오히려 하락한다.

 

따라서, 본 논문에서는 반대로 uncertainty가 높은 부분에 더 weight를 주는 방식을 고안한다. 1)에서 계산된 uncertainty를 이용해, L1 loss에 곱해준다. 즉, 1)에서 uncertainty를 계산하는 network를 훈련시키고, 2)에서는 이를 이용해 uncertainty weight를 주어 새롭게 network를 훈련시키는 것이다. 이 때 사용하는 loss는 다음과 같다.

 

$\mathcal{L}_{UDL}=\frac1N\sum_{i=1}^N\hat{s_i}||x_i-f(y_i)||_1$

 

여기서 $\hat{s_i}=s_i-\min(s_i)$가 각 sample에 대한 L1 loss의 weight로 사용된다. $s_i$는 1)에서 학습된 network에서 얻어진 uncertainty 값으로, 2)의 network를 훈련시킬 때 1)의 network는 fix해둔 상태로 사용한다. Uncertainty의 scaling 함수는 이외에도 다양한 경우를 실험해 봤는데, 이는 result section에서 소개하겠다. 

 

추가로, 2)의 network의 훈련은 1)에서 훈련된 weight를 가져와서 이어서 학습시킨다.

 

 

 

4. Experiments

DIV2K dataset을 이용해 3가지의 모델을 훈련시켰다. 사용한 모델은 다음과 같다.

• EDSR-S
• DPDNN
• EDSR

 

정성적, 정량적 평가에서 모두 proposed method가 가장 좋은 성능을 보였다. Uncertainty map을 추가로 report 했다.

 

 

사용한 Loss에 대한 ablation study도 진행했다. 본 논문에서는 estimating sparse uncertainty (ESU) loss와, SISR을 위한 uncertainty-driven loss (UDL) 두 가지를 제안한 셈인데, UDL loss를 썼을 때 성능이 올라가는 것은 물론이고, uncertainty 측정을 위해 기존의 loss (EU)를 사용했을 때 보다 ESU loss를 사용했을 때 더 성능이 좋았음을 함께 보인다. 이는 ESU loss가 EU loss보다 uncertainty 를 더 잘 측정하기 때문이라고 설명한다.

 

 

Uncertainty 외에도 pixel의 variance를 나타낼 수 있는 방법은 여러가지가 있다. Error map을 이용해도 되고, gradient map을 이용해도 된다. 따라서 uncertainty 대신 이들을 이용해 loss에 weight을 줬을 때도 효과가 있는지를 조사했다. 결과는 모두 baseline보다 어느정도 성능이 향상되기는 하지만, uncertainty를 이용했을 때가 가장 성능이 높았고, 이는 uncertainty가 pixel의 variance를 가장 잘 나타냄을 의미한다. Error map은 semantic information이나 local information을 충분히 표현하지 못하며, gradient map은 edge만을 표현할 뿐 complex texture detail은 표현하지 못하기 때문이다.

 

 

이외에도 UDL loss에 이용하기 위한 uncertainty의 scaling 방법에 대한 비교도 진행한다. 여러 방법을 비교해 본 결과 모두 baseline보다는 성능이 향상됐으며, linear scaling (2nd column)과 log scaling (5th column)이 가장 성능이 좋았는데 이 중 계산량이 적은 linear scaling을 채택했다고 한다.

 

 

5. PyTorch Implementation

https://github.com/QianNing0/UDL

GitHub - QianNing0/UDL: PyTorch code for NeurIPS2021 paper "Uncertainty-Driven Loss for Single Image Super-Resolution"

 

Train step1과 step2에 해당하는 모델을 각각 구현했다.

 

Step1의 모델은 다음과 같다.

#https://github.com/QianNing0/UDL/blob/main/code/model/edsr.py로부터 일부 수정

class EDSR(nn.Module):
    def __init__(self, n_colors, n_feats, kernel_size, n_resblock):
        super(EDSR, self).__init__()
        
        self.head = nn.Conv2d(n_colors, n_feats, kernel_size)
        self.body = nn.Sequential(*[ResBlock(n_feats, kernel_size) for _ in range(n_resblock)])
        
        self.tail = nn.Sequential(*[Upsampler, nn.Conv2d(n_feats, n_colors, kernel_size)])
        self.var_conv = nn.Sequential(*[
            nn.Conv2d(n_feats, n_feats, kernel_size),
            nn.ELU(),
            nn.Conv2D(n_feats, n_feats, kernel_size),
            nn.ELU(),
            nn.Conv2d(n_feats, n_colors, kernel_size),
            nn.ELU()
        ])
        
    def forward(self, x):
    
        x = self.head(x)
        res = self.body(x)
        res += x
        
        x = self.tail(res)
        var = self.var_conv(nn.Functional.interpolate(res), mode='nearest')
        return [x, var]

 

Head-body-tail은 EDSR network와 동일하다. var_conv는 tail과 동일한 input을 받아 nearest upsampling을 한 후 conv layer+ELU activation function들을 거쳐서 aleatoric uncertainty map을 계산한다.

 

 

Step2의 모델은 다음과 같다.

#https://github.com/QianNing0/UDL/blob/main/code/model/edsr_two.py로부터 일부 수정

class EDSR_two(nn.Module):
    def __init__(self, n_colors, n_feats, kernel_size, n_resblock, pre_train_step1):
        super(EDSR_two, self).__init__()
        
        self.EDSR_var = EDSR(n_colors, n_feats, kernel_size, n_resblock)
        self.EDSR_U = EDSR(n_colors, n_feats, kernel_size, n_resblock)
        
        self.EDSR_var.load_state_dict(torch.load(pre_train_step1), strict=True)
        self.EDSR_U.load_state_dict(torch.load(pre_train_step1), strict=True)
        
    def forward(self, x):
        with torch.no_grad():
            _, var = self.EDSR_var(x)
        x, _ = self.EDSR_U(x)
        return [x, var]

 

step1의 모델을 그대로 사용해 하나는 uncertainty를 계산하는 용도로, 하나는 새롭게 train하는 용도로 사용한다.

EDSR_var은 gradient를 계산하지 않고 freeze하여 uncertainty만 얻고,

EDSR_U는 동일한 weight로부터 이어서 다시 학습시킨다.

 

 

Loss 부분의 코드는 다음과 같다. 

#다음의 코드로부터 일부 수정
#1) https://github.com/QianNing0/UDL/blob/main/code/trainer.py
#2) https://github.com/QianNing0/UDL/blob/main/code/loss/__init__.py

loss_f = nn.L1Loss()

lr, hr = # low resolution & high resolution
sr, var = model(lr)

if stage == 'step1':
    #calculate ESU loss
    s = torch.exp(-var)
    sr_ = torch.mul(sr, s)
    hr_ = torch.mul(hr, s)
    loss = loss_f(sr_, hr_) + 2*torch.mean(var)
    
elif stage == 'step2':
    #scaling variance (hat_s in the paper)
    var_ = var.view(var.size(0), var.size(1), -1) #b, c, h*w
    pmin = torch.min(var_, dim=-1)[0] #b, c
    pmin = pmin.unsqueeze(-1).unsqueeze(-1) #b, c, 1, 1
    s = var - pmin + 1
    
    #calculate UDL loss
    sr_ = torch.mul(sr, s)
    hr_ = torch.mul(hr, s)
    loss = loss_f(sr_, hr_)