NeurIPS 2020에서 발표된 CSI: Novelty Detection via Contrastive Learning on Distributionally Shifted Instances 라는 논문이다. Out-of-distribution detection에 SimCLR을 토대로 한 contrastive learning을 적용하였다.
논문: https://arxiv.org/pdf/2007.08176.pdf
코드: https://github.com/alinlab/CSI
Abstract
Novelty detection이라고도 부르는 Out-of-distribution (OOD) detection은, 주어진 sample이 training distribution 내부의 것인지 (in-distribution), 외부의 것인지 (out-of-distribtuion)을 판단하는 문제이다.
본 논문에서는 contrastive learning을 이용한 Contrasting shifted instances (CSI) 라는 방법을 제안하며, 이는 각 sample 뿐만 아니라 distributionally-shift augmented sample 역시 contrast (대조) 대상으로 두는 방법이다. 이에 추가로, 제안한 방법에 알맞는 detection score을 제안한다.
1. Introduction
Out-of-distribtuion (OOD) detection.
Out-of-distribtuion (OOD) detection이란, 어떠한 test input이 training distribution 으로부터 온 것인지 (in-distribution), 아닌지 (out-of-distribution)을 판단하는 문제이다. 일반적으로, 학습 과정에서는 training data만 주어지며, OOD sample space는 매우 크기 때문에, OOD space에 대한 특정한 prior knowledge를 이용하려는 시도는 오히려 특정 OOD에 대한 bias만 심어줄 수 있다. OOD detection은 medical domain이나 autonomous driving, industrial 등에서 유용하게 사용될 수 있다. OOD detection에 대한 보다 자세한 설명은 다음 링크를 참고 바람. (link)


Previous works.
OOD detection을 하기 위한 많은 시도들이 있었는데, 그 중 하나는 one-class classification이다. 이는 training sample 끼리 최대한 가까워지게 하는 feature mapping 을 학습한다. Test sample에 대하여, feature space 에서 center point 와 멀리 떨어져 있을수록 out-of-distribution, 가까울 수록 in-distribution에 가깝다고 판단한다. One-class classifier에 대한 보다 자세한 설명은 다음 링크를 참고 바람 (link)

또 다른 방법은 Autoencoder를 이용한 방법이다. Training sample들을 이용해 input image를 압축한 뒤 다시 원래의 image로 복원하는 autoencoder를 이용하고, test sample에 대해 autoencoder로 복원한 결과와의 차이를 비교해 reconstruction error이 높을 경우 out-of-distribution으로 판단한다.

본 논문에서는 contrastive learning을 이용해 OOD detection을 수행한다. Contrastive learning이란, 비슷한 여러 개의 view의 sample들끼리 서로 attract하고, 다른 sample들끼리는 repell하도록 함으로써 strong inductive bias를 추출하는 방법이다. 이 중 Instance discrimination은 contrastive learning의 한 종류로, 여러 개의 view를 만드는 방법으로 서로 다른 augmentation들을 사용한다.

일반적인 contrastive learning은 in-distribution에서의 각 sample들을 구별하는 것이 목적인 반면, 본 논문에서 제안하는 CSI는 in-distribution과 OOD sample들을 서로 구별하는 것이 목적이다. CSI는 "hard" augmentation들을 활용하는 방식으로 contrastive learning을 수정하여 OOD detection에 사용한다.
2. Method
Problem definition.
우선, OOD detection에 대한 problem definition은 다음과 같다.
- 전체 data space를 라 하고, data distribution 에서 sample된 Dataset을 라고 하자.
- 이 때, OOD의 목적은 가 in-distribution 에서 sample된 것인지 아닌지를 판별하는 detector 을 modeling하는 것이다.
- 를 바로 modeling하는 것은 어렵기 때문에 많은 방법들은은 score function 을 정의하여 사용한다.
Contrastive learning.
본 논문에서 제안하는 방법은 Contrastive learning을 이용하고 있다. Contrastive learning이란, 서로 비슷한 sample들과 그렇지 않은 sample들을 구분함으로써 중요한 정보들을 추출할 수 있는 encoder 를 학습하는 방법이다.
- 를 query, 와 를 각각 positive sample과 negative samples의 set이라 하고,
- 을 consine similarity라 하자.
- 이 때, contrastive loss의 기본 형태는 다음과 같이 된다:
-
- : cardinality of the set
- : output feature of the contrastive layer
- It can be defined by applying an additional projection layer :
- It can be defined by applying an additional projection layer :
- : temperature (hyperparameter)
-

SimCLR.
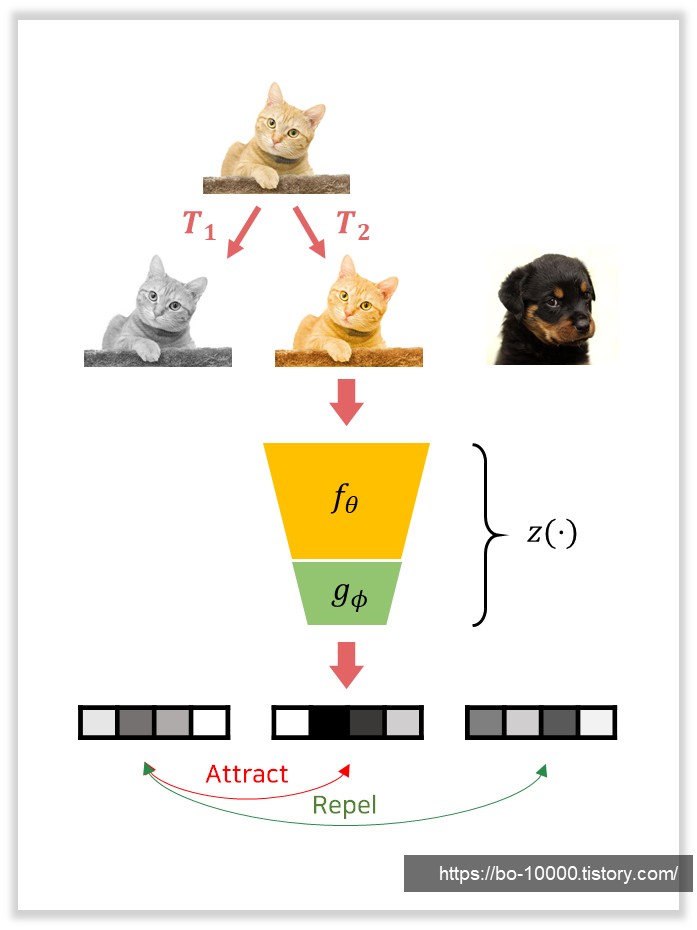
본 논문에서는, instance discrimination을 이용한 SimCLR를 토대로 삼고 있다.
- 와 를 pre-defined augmentation family 에서 온 의 서로 다른 augmentation들이라고 하자.
- i.e., , , where .
- 이 때 SimCLR objective는 와 를 query-key pair로 하고 나머지를 negative로 하는 contrastive loss를 이용해 정의할 수 있다.
- Batch 에 대해, objective는 다음과 같이 정의된다:
-
CSI.
SimCLR에서는, 어떠한 augmentation family 를 사용했을 때 더 나은 representation을 학습할 수 있는지에 대한 실험을 진행했다. 즉, encoder 가 어떤 transformation을 postive로 두었을 때 더 좋은 성능을 보이는지에 대한 실험이다. 그 결과, rotation을 포함한 일부 augmentation들은, SimCLR의 성능을 오히려 떨어트릴 수도 있다는 결론이 도출되었다.

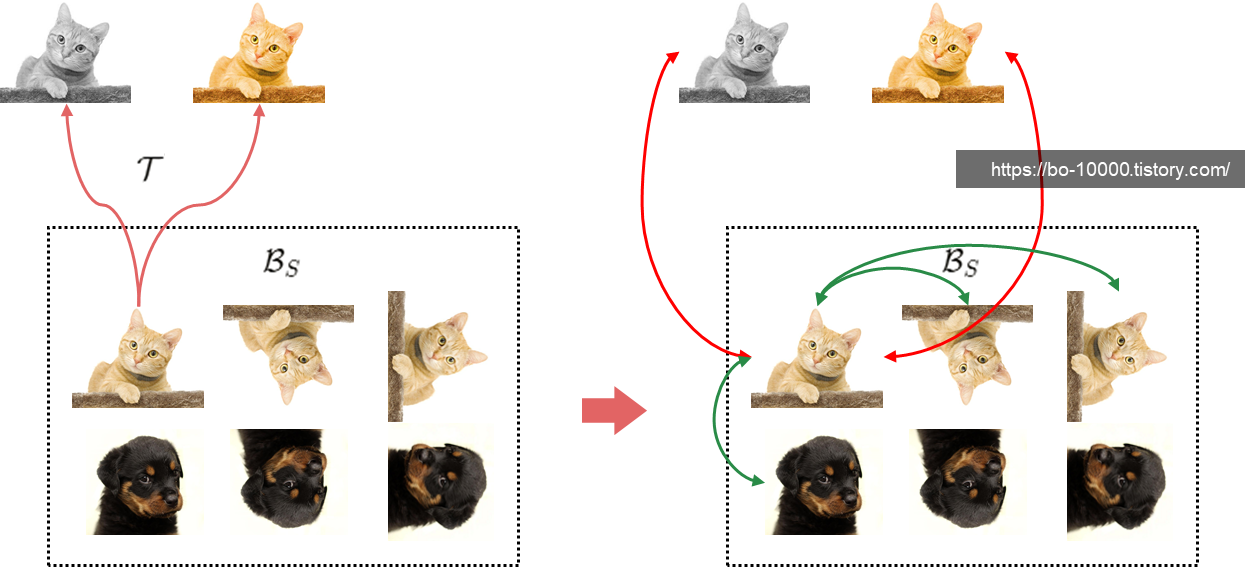
본 논문에서는, 그러한 augmentation들을 negative sample로 활용함으로써 OOD detection에 유용하게 사용될 수 있을 것으로 보았다. CSI는 그러한 augmentation family를 (distribution-) shifting transformation 이라 정의한다.
CSI objective는 두 단계로 구성된다. 우선, 가장 중요한 부분인 con-SI는 다음과 같다. 이는 contrastive learning의 역할을 하는 loss이다.
- Identity 를 포함해, 개의 서로 다른 transformation을 포함하는 set 을 정의한다:
- Augmented sample들을 positive로 고려하는 SimCLR과 달리,
- CSI는 만약 augmentation이 로부터 왔다면, 그들을 negative로 고려한다.
- 이때 contrasting shifted instances (con-SI) loss는 다음과 같다:
-
- 이 때 각 distributionally-shifted sample (i.e., ) 들은, OOD로 간주된다.
- 또한, con-SI는 in-distribution (i.e., ) sample과 OOD (i.e., ) sample들을 서로 구분하려고 한다.
- 참고로, 이 방법은 standard clsasification의 representation을 개선시키지는 않는다. 단지 OOD detection의 representation의 성능을 개선시킬 뿐이다.
-
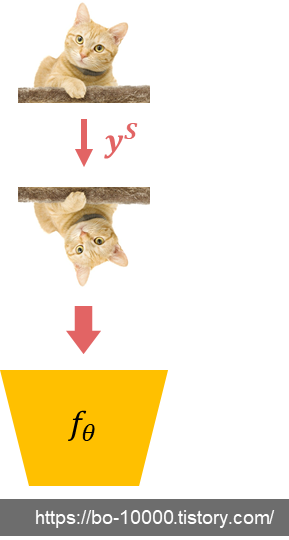
두 번째 단계인 cls-SI는 다음과 같다. 이는 auxiliary classifier을 이용한 loss이다.
- Given input 에 대해, 어떤 shifting transformation 이 가해졌는지를 맞추는 auxiliary task를 추가로 정의한다.
- 이를 위해, 다른 연구들과 마찬가지로 auxiliary softmax classifier 를 modeling하기 위한 linear layer을 에 추가한다.
- 를 SimCLR을 통해 augment된 batch 라고 하자. 이 때 classifying shifted instances (cls-SI) loss는 다음과 같다:
최종 loss는 위 두 loss의 weighted sum으로 구성된다.
본 논문에서는 로 설정하여 실험을 진행했다.
SupCLR.
여기에 추가로, in-distribution의 class를 예측하는 extension을 함께 제안한다. Labeled dataset 이 주어졌을 때, classification의 confidence를 높일 수 있는 confidence-calibrated classifier을 학습하기 위해, supervised contrastive learning (SupCLR)을 이용한다. Confidence-calibrated classifier의 목적은 다음과 같다:
- accurate on predicting y when x is in-distribution,
- the confidence is well-calibrated, i.e., should be low if is an OOD sample or true label.
SupCLR은 SimCLR의 supervised extension으로, 각 sample을 instance-wise가 아닌 class-wise하게 대조한다. 같은 class에 속한 sample들은 positive로 두고, 다른 class에 속한 sample들은 negative로 둔다. Embedding network 의 학습이 끝난 후에, 을 modeling하기 위한 linear classifier을 에 대하여 학습한다.
CSI의 Supervised extenstion (SupCLR)은 다음과 같이 정의된다.
How to choose shifting transformation?
Shifting transformation으로 어떤 것을 이용할 지는, vanilla SimCLR을 이용해 각 transformation의 OOD-ness를 측정하여 사용한다. OOD-ness를 측정하는 방법은, OOD detection score을 통해 in-distribution과 transformed sample 간의 AUROC를 측정하면 되는데, 본 논문에서는 새로운 OOD detection score 두 가지를 제시하고, 이 중 첫 번째를 shifting transormation을 정하기 위한 OOD-ness를 측정하는 데에 사용하고, 두 번째를 실제로 test 단계에서 OOD detection을 하는 데에 사용한다.
첫 번째 방법은 SimCLR representation의 feature들을 이용한 방법이다. 본 논문의 저자들은 두 가지의 feature이 OOD sample을 탐지하는 데에 매우 유용함을 발견했다.
A. the cosine similarity to the nearest training sample in :
Training sample 중, feature space에서 가장 가까운 sample과의 cosine similarity이다. In-distribution sample들의 경우, 해당 값이 거의 1.0에 가까운 반면, OOD sample들의 경우 그 값의 분포가 훨씬 작았다. 그 이유는 SimCLR가 각 sample들 간의 거리가 최대한 멀어지는 방향으로 학습하지만, 비슷한 sample들의 경우 그 거리가 가까워지기 때문에 (t-SNE에서 이를 확인할 수 있다) in-distribution sample들의 경우 "가장 가까운" sample과의 거리는 가깝게 되는 것이다. 반면 OOD sample들의 경우, training set에서 비슷한 sample이 없기 때문에 그 거리가 상대적으로 멀어진다 ((c) 그림 참고).
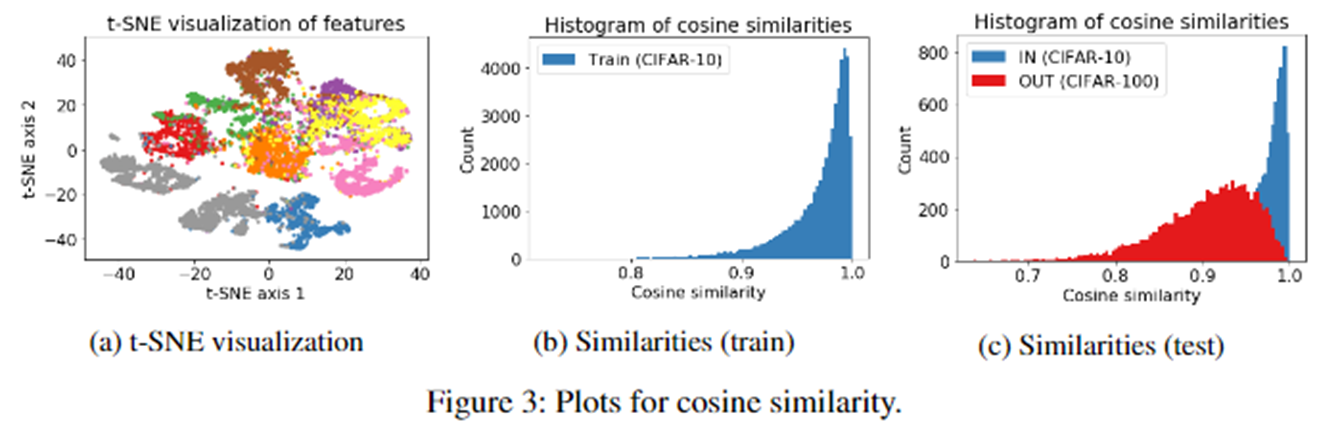
B. the norm of the representation:
두 번째는 representation의 norm이다. SimCLR의 objective에는 각 vector가 normalize되어 들어가기 때문에 (cosine similarity 수식을 보면 알 수 있다) in-distribution과 OOD의 norm 값에 차이가 나는게 의아할 수 있다. 본 논문의 저자들은 이들을 다음과 같이 설명한다. "두 vector 간의 cosine similarity를 최대화하기 위한 쉬운 방법은, 두 vector의 norm을 키우는 것이다. 두 feature 간의 거리를 direct하게 줄이는 것보단, 전체 norm을 키우는 것이 relative distance를 줄이기 위해 더 쉬운 방법을 제공한다." (직관적으로 보자면 이 설명이 이해가 가고, 결과적으로 봤을 때 OOD sample의 전체적인 norm이 in-distribution sample보다 작다 ((b), (c) 그림 참고). 또한 norm을 score로 했을 때 실제로 epoch가 늘어날 수록 AUROC가 증가하는 것을 확인할 수 있다 (a). 실험결과와 직관적인 설명이 이를 뒷받침하지만 수학적으로 증명되지 않아 아쉽다.)

이 둘을 결합하여, 최종 detection score 은 다음과 같이 정의된다.
앞서 말했다시피 이 score의 AUROC를 vanilla SimCLR에 적용해 shifting transformation을 결정했고 (=OOD-ness), 그 결과는 다음과 같다. 실험대상은 perm을 제외하고는 모두 SimCLR에서 성능을 떨어트린다고 보고된 바 있는 augmentation들이며, CIFAR-10을 dataset을 이용해 실험을 진행하였다.

표에서 볼 수 있듯이, Rotate의 OOD-ness가 제일 높았기 때문에, 0, 90, 180, 270도 rotation을 shifting transformation으로 사용했다.
두 번째 방법은 CSI를 이용했을 때 사용 가능한 score이다. 두 가지의 추가적인 score이 정이되는데, 이들은 다음과 같다.
-
- : balancing term to scale the scores of each shifting transformation.
- it is an expectation of over .
-
- : balancing term
- : weight vector in the linear layer of per
- If the confidence of correct transformation is high, then the score is high.
CSI representation을 이용한 최종 score은 다음과 같다.
3. Experiments
Setup.
Backbone으로 ResNet-18을 사용했고, positive sample을 생성하기 위한 data augmentation 로는 inception crop, horizontal flip, color jitter, grayscale을 이용했다.

shifting transformations 의 경우 앞서 언급한 바와 같이 random rotation 0, 90, 180, 270를 사용했다.
Unlabeled one-class datasets.
하나의 dataset을 이용해, 하나의 class는 in-distribution으로 두고 나머지 class를 OOD로 두어 실험하였다.

Unlabeled multi-class datasets.
하나의 데이터셋을 in-distribution으로, 다른 데이터셋을 OOD로 두어 실험하였다.

Labeled multi-class datasets.
Unlabeled multi-class dataset과 동일한 setting이나, classification task를 추가로 수행하기 위해 앞서 언급한 Sup-CSI를 이용했다.

Ablation study.
Shifting transformation과 관련된 다양한 ablation study를 진행했다.
첫 번째는 다양한 shifting transformation에 따른 성능이다. Rotation 외에도, cutout, sobel, noise, blur, perm, rotate를 이용해 모델을 학습하고 성능을 기록했는데, OOD-ness와 거의 비례하게 OOD detection 성능이 나옴을 확인할 수 있다 (Table 5 (a), second row). 또한, 해당 augmentation들을 shifting transformation이 아닌, 일반 augmentation으로 사용해, positive sample을 만드는 데에 사용한 결과 성능이 baseline에 비해 떨어짐을 확인할 수 있다 (Table 5 (a), first row). 이는 SimCLR에서 제시한 결과와 동일하다. 또한, SimCLR에서 사용한 augmentation들 중 일부를 제거하거나, 이를 shifting transformation으로 실험한 결과도 있는데 (Table 5 (b)), 이를 통해 각 augmentation을 positive sample을 만드는 데에 이용하거나, negative sample을 만드는 데에 이용함으로써 성능이 차이가 날 수 있음을 알려주고 있다.

또한, 본 논문에서는 rotation을 best shifting transformation으로 사용했지만, 이는 dataset에 따라 차이가 날 수 있다고 얘기한다. 예를 들어, rotation-invariant dataset (ex: textile dataset, aerial images) 의 경우 Rotation이 best shifting transformation이 아닐 수도 있다. 이를 보이기 위해 DTD와 Textile dataset을 이용한 실험을 진행했다. 두 dataset 모두 rotation-invariant 한 dataset으로, rotation을 shifting transformation으로 사용했을 때 성능이 좋지 않았고, 대신 gaussian noise를 사용했을 때 좋은 성능을 보였다.

마지막으로, training objective를 하나씩 제거해가며 비교한 결과와, 여러 detection score을 이용한 결과를 첨부한다. 당연하게도 논문에서 제시한 training objective와 detection score을 사용했을 때 결과가 가장 좋다.
