[딥러닝 논문리뷰] PointMLP - Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP Framework (ICLR 2022)

ICLR 2022에서 발표된 Pointcloud analysis를 위한 모델이다. 기존 Pointcloud analysis 모델들은 복잡한 local geometric extractor들을 이용해 왔는데, 이들과 달리 매우 간단한 구조로 SOTA를 달성할 수 있음을 보였다.

 

Paper, Code

 

 

1. Introduction 

기존 pointcloud 모델들은 3D geometric을 포착하기 위해 convolution, graph, attention 등 매우 복잡한 local geometric extractor들을 이용했는데, 이들은 computational overhead가 너무 크다는 단점이 있다.

 

저자들은 pointcloud analysis의 핵심은 detailed local geometrical information을 포착하는 것이 아니라고 판단하여, 복잡한 local geometric extractor 없이 residual feed-forward MLP만을 이용하는 PointMLP로 point cloud analysis에서 SOTA를 달성한다. 이는 real-world application에서 지금까지도 가장 많이 사용되는 PointNet이나 PointNet++와 유사한 구조를 채택했다고 볼 수 있다.

 

 

 

 

3. Method

PointNet++ and its variants

 

PointMLP를 설명하기 전에 PointNet++의 구조를 먼저 살펴보면, PointNet++은 여러 learning stage를 stack함으로써 pointcloud data의 hierarchical한 feature을 학습한다.

 

각 $s$번째 stage에서, $N_s$ 개의 point들이 farthest point sampling (FPS)를 통해 추출되고, 각 point의 $K$개의 neighbor들을 aggregate하여 local structure의 feature을 추출한다. 이를 식으로 나타내면 다음과 같다.

 

• $g_i=\mathcal A(\Phi(f_{i,j}|j=1,...,K)$
  • $\mathcal A$: aggregation function (Max-pooling)
  • $\Phi$: local feature extractor (MLP)
  • $f_{i,j}$: $i$번째 sampled point의 $j$번째 neighbor point feature

 

PointNet++에서는 local feature extractor $\Phi$로 MLP를 이용했지만, conv, graph, attention 등 다양한 구조를 사용하는 시도들이 있어 왔다.

 

이들은 detailed local geometric information을 포착할 수 있다는 장점이 있지만, computational complexity가 매우 높고, local feature extractor의 구조를 개선시킴으로써 얻을 수 있는 performance gain이 점점 포화상태가 되어가고 있다는 문제가 있다.

 

 

PointMLP

 

PointMLP의 key operation은 다음과 같다.

 

• $g_i=\Phi_{pos}(\mathcal A(\Phi_{pre}(f_{i,j},|j=1,...,K))$
  • $\Phi_{pre}$, $\Phi_{pos}$: residual point MLP blocks, i.e., MLP(x) + x
    • $\Phi_{pre}$: learn shared weights from a local region
    • $\Phi_{pos}$: extract deep aggregated features
  • $\mathcal A$: aggregation function (max-pooling)

 

이 operation을 $s$ stage에 걸쳐 반복한다. 실험에서는 4 stage를 이용했다. 자세한 구조는 다음과 같다.

 

 

이 방법의 이점은 다음과 같다.

1. MLP를 이용하기 때문에, permutation invariant하다. 이는 PointNet에서도 강조한 feature이다.
2. Residual connection을 사용함으로써 layer 깊이를 깊게 늘릴 수 있다.
3. 복잡한 local feature extractor을 이용하지 않아도 되어, 계산이 효율적이다.

 

 

Geometric Affine Modules

이처럼 단순한 구조의 deep MLP만을 이용하면 좋은 성능을 얻기 힘들다. 각 local 영역에는 다양한 geometric structure가 있는데, 하나의 shared MLP만을 이용해서 이들의 특성을 추출하는 것은 쉽지 않다. 이를 해결하기 위해 geometric affine module을 도입한다. 

 

$\{f_{i,j}\}_{j=1,...,k}\in\mathbb R^{k\times d}$를 $f_i$의 grouped local neighbor이라 하자. 이 때 총 point의 수는 $k$개이고, 각 neighbor point $f_{i,j}$는 dimension $d$의 vector이다.

 

이 local neighbor point들을 다음과 같이 normalization시킨다.

 

• $\{f_{i,j}\}=\alpha\odot\frac{\{f_{i,j}\}-f_i}{\sigma+\epsilon}+\beta$
  • $\sigma=\sqrt{\frac1{k\times n\times d}\sum_{i=1}^n\sum_{j=1}^k(f_{i,j}-f_i)^2}$: feature deviation across all local groups and channels
  • $\alpha,\beta\in\mathbb R^d$: learnable parameters

 

 

4. Results

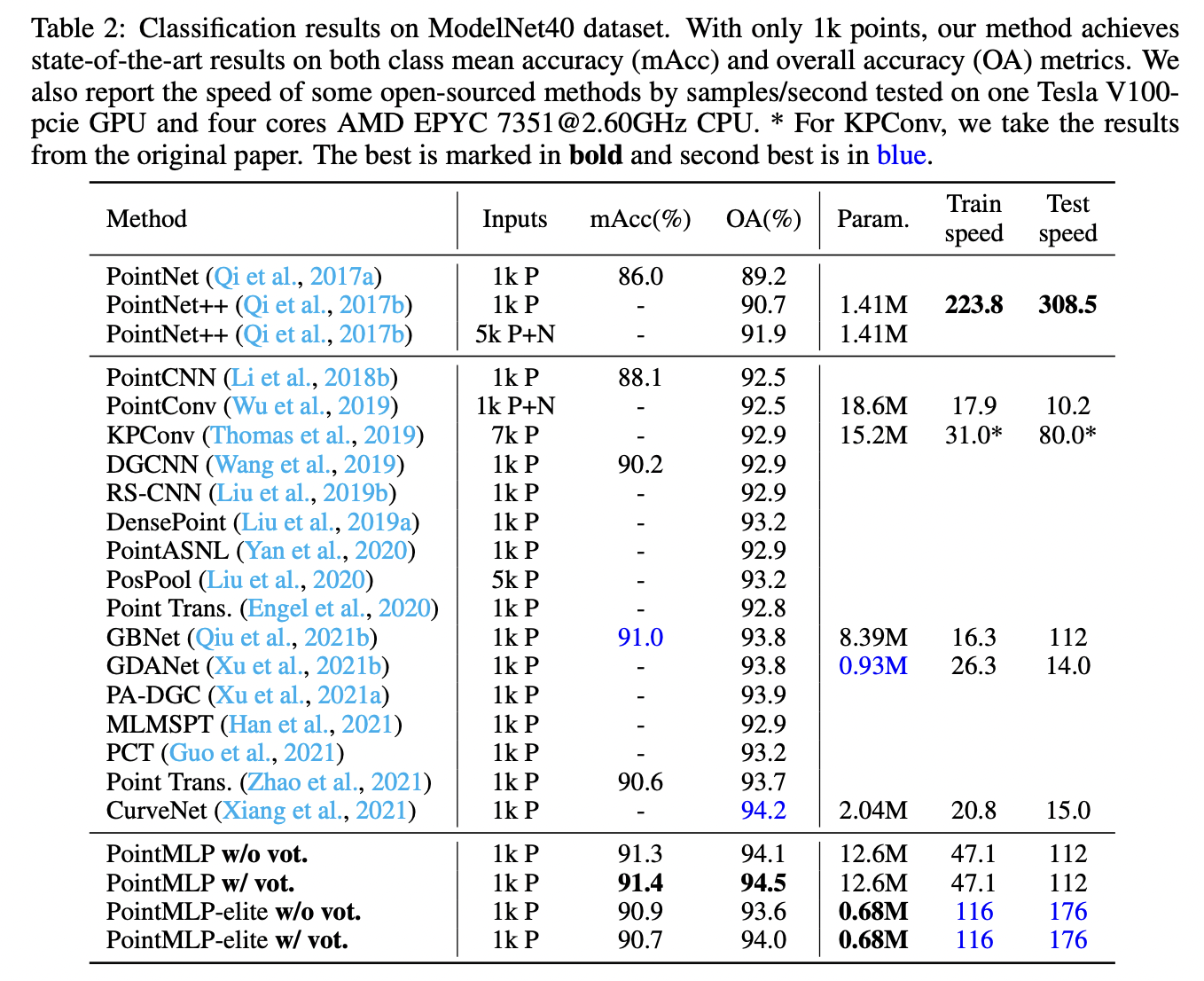
ModelNet40 데이터셋을 이용한 classification 결과이다. 맨 아래의 PointMLP-elite는 구조를 일부 수정해 더 가볍게 만든 버젼이다. Random하게 1024개의 point를 추출했고, data augmentation의 경우 PointNet++과 동일한 것을 사용했다.

 

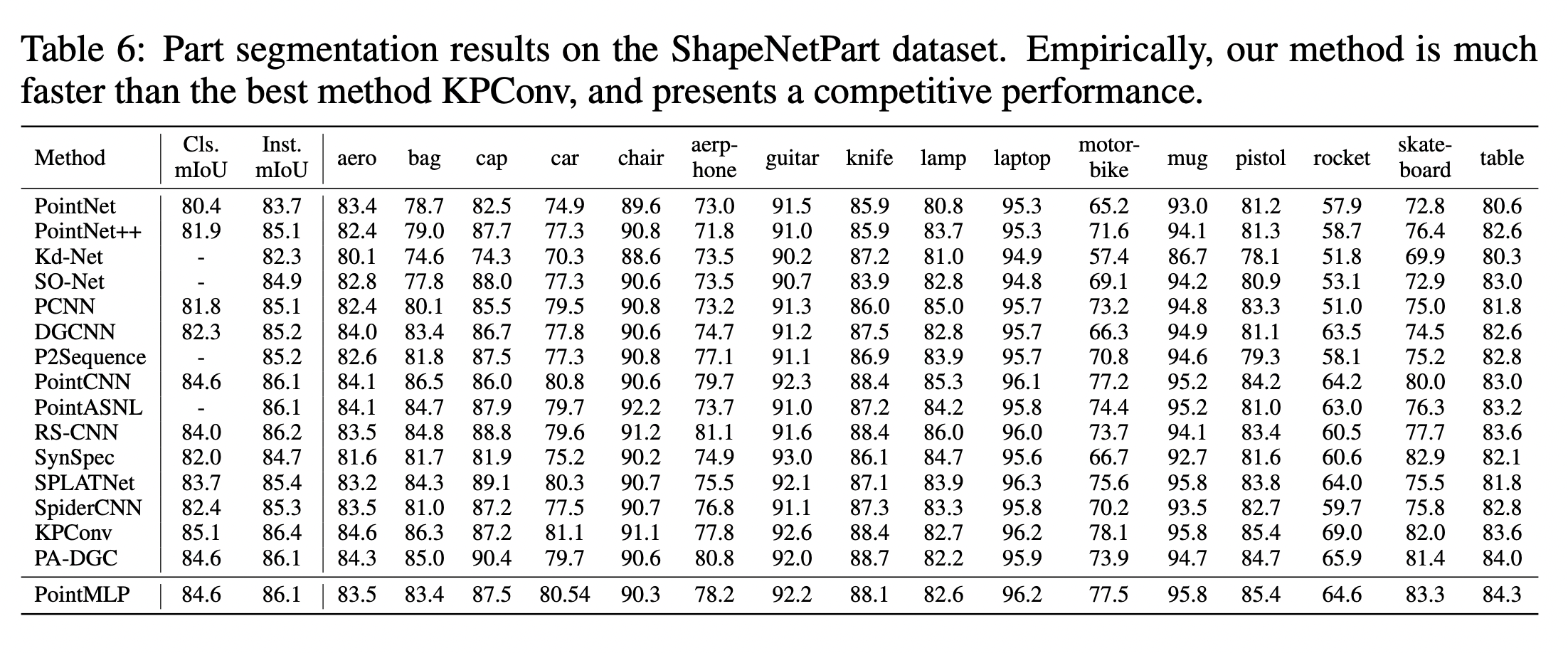
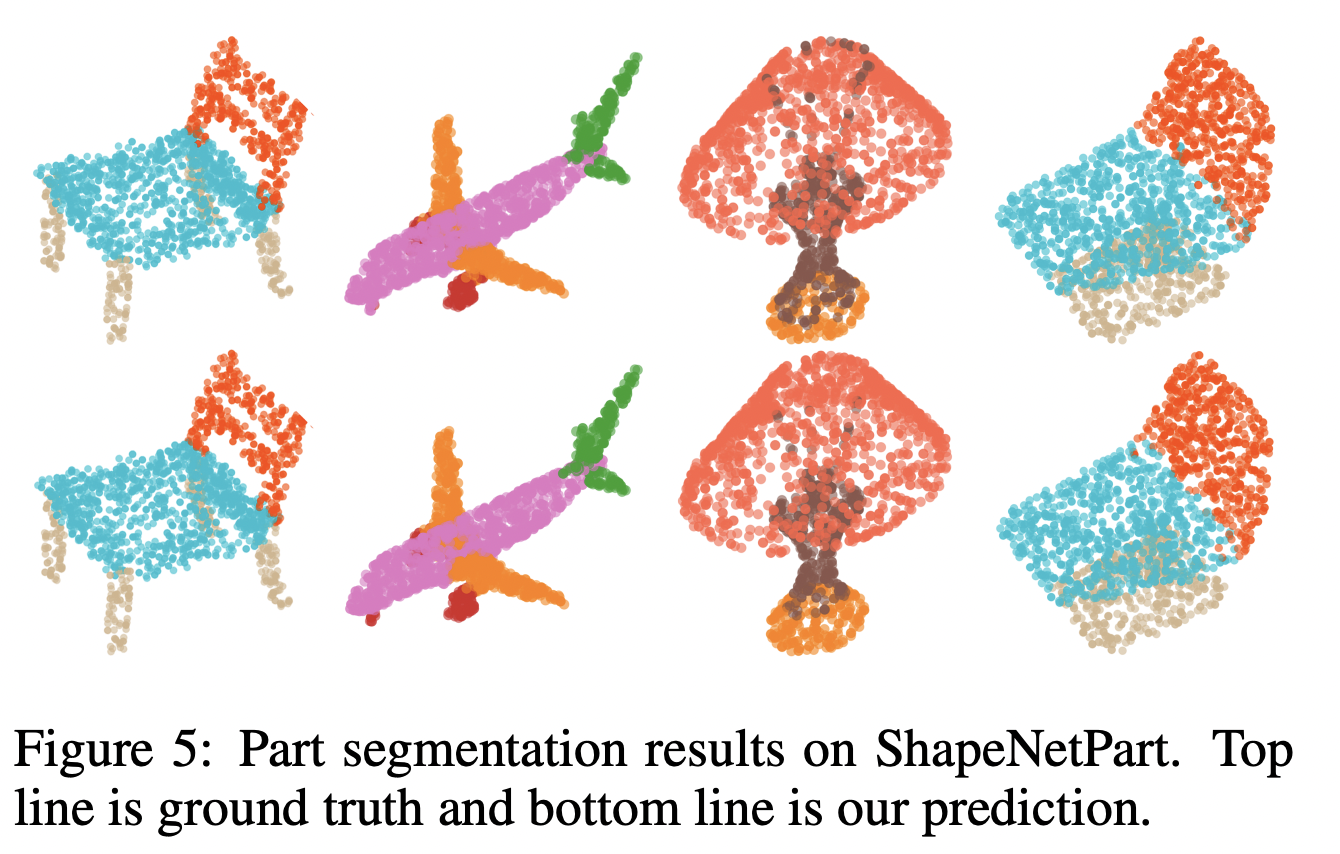
다음은 ShapeNetPart 데이터셋을 이용한 part segmentation 결과이다. Figure 5의 위가 ground truth이고, 아래는 PointMLP로 예측한 결과이다.