[딥러닝 논문리뷰] MeZO: Fine-Tuning Language Models with Just Forward Passes (NeurIPS 2023)

논문 링크: https://arxiv.org/pdf/2305.17333.pdf

발표 영상: https://neurips.cc/virtual/2023/poster/71437

코드: https://github.com/princeton-nlp/MeZO

NeurIPS 2023

 

(L)LM fine-tuning에는 메모리가 많이 든다. Adam을 이용한 backpropagation은 inference의 약 12배 정도의 메모리가 필요하다. 이를 해결하기 위해 inference와 동일한 크기의 메모리로 LM을 fine-tuning할 수 있는 MeZO를 제시한다.

 

 

1. Introduction

(L)LM fine-tuning에는 메모리가 많이 든다. (Adam: inference의 12배정도) 왜냐면 Adam과 같은 optimizer들은 forward activation, backward gradient, gradient history 등을 다 기록해둬야 하기 때문이다. 이때문에 A100 GPU 사용 시 inference만 하면 30B LLM을 돌릴 수 있지만, Adam을 이용한 backpropagation은 2.7B LLM이 한계이다.

 

 

prompt engineering을 통한 In-context learning (ICL)의 경우 single inference만으로 모델을 fine-tune할 수 있지만, 직접 backpropagation을 통해 모델 weight를 업데이트 하는 것보다는 성능이 떨어질 수밖에 없다.

 

ZO-SGD(zeroth-order optimization) 방법은 loss value 간의 차이만을 이용해 gradient를 추정한다. 그러나 이 방법은 여전히 inference의 두 배에 해당하는 메모리가 필요하며 모델 사이즈가 커질수록 수렴이 느려진다고 알려져 있다. 때문에 LM 학습에는 직접적으로 활용된 바가 없다.

 

MeZO(memory-efficient zeroth-order optimizer)는 inference와 동일한 크기의 메모리만을 이용해 모델을 업데이트한다. MeZO는 billion 규모의 파라미터를 가진 LM을 성공적으로 fine-tuning 하는데에 성공했다.

 

 

2. Method

MeZO는 ZO-SGD에 기반을 두고 있다. SPSA는 ZO에서 사용하는 클래식한 gradient estimator로, 단 두 번의 forward pass만을 이용해 gradient를 추정할 수 있다.

 

 

SPSA의 gradient 추정 방법은 다음과 같다.

• Randon direction $z$가 샘플링된다.
• 모델의 parameter들은 $\pm z$ 방향으로 perturb된다.
• 각 방향에서 계산된 loss를 이용하면, $\epsilon \rightarrow 0$ 일 때, 위 식을 이용해 loss를 근사할 수 있다.

 

이렇게 추정한 gradient를 이용하면 아무 optimizer나 이용해서 parameter update를 할 수 있다. SGD에 사용하는 예시는 다음과 같다.

 

 

그런데, SPSA는 inference의 두 배 메모리가 필요하다. 그 이유는 매번 sampling하는 $z$의 크기가 parameter의 전체 크기와 동일하기 때문이다.

 

$z \sim \mathcal N(0, I_d)\in \mathbb R^d$

 

MeZO의 알고리즘은 다음과 같다.

 

 

1. Random seed s를 뽑는다.
2. Parameter perturbation은 in-place로 진행되는데, 매번 parameter perturbation을 할 때마다 random number generator을 초기화한다.
3. Parameter perturbation은 parameter 하나씩 iteration을 돌면서 진행되는데, 매 iteration마다 각각의 parameter의 perturbation에 사용될 z를 random number generator을 이용해 뽑는다.
4. 첫번째 parameter perturbation: +$\epsilon$ 만큼 perturb해서 +방향의 loss 계산
5. 두번째 parameter perturbation: -2$\epsilon$ 만큼 perturb해서 -방향의 loss 계산
6. 세번째 parameter perturbation: -$\epsilon$ 만큼 perturb해서 원래대로 복귀
7. +- 방향의 loss 이용하여 SPSA로 gradient 추정, parameter update

 

이 방법을 이용하면 random seed $s$만을 저장하고도 ZO를 구현할 수 있다.

 

코드는 다음과 같다.

 

# https://github.com/princeton-nlp/MeZO/blob/main/large_models/trainer.py#L757C1-L788C21
def zo_step(self, model, inputs):
    """
    Estimate gradient by MeZO. Return the loss from f(theta + z)
    """
    args = self.args

    # What parameters to optimize 
    self.named_parameters_to_optim = []
    for name, param in model.named_parameters():
        if param.requires_grad:
            self.named_parameters_to_optim.append((name, param))

    # Sample the random seed for sampling z
    self.zo_random_seed = np.random.randint(1000000000)

    # First function evaluation
    self.zo_perturb_parameters(scaling_factor=1)
    loss1 = self.zo_forward(model, inputs)

    # Second function evaluation
    self.zo_perturb_parameters(scaling_factor=-2)
    loss2 = self.zo_forward(model, inputs)

    self.projected_grad = ((loss1 - loss2) / (2 * self.args.zo_eps)).item()

    # No gradient accumulation support
    assert self.args.gradient_accumulation_steps == 1

    # Reset model back to its parameters at start of step
    self.zo_perturb_parameters(scaling_factor=1)
    
    return loss1


# https://github.com/princeton-nlp/MeZO/blob/main/large_models/trainer.py#L699C1-L712C76
def zo_perturb_parameters(self, random_seed=None, scaling_factor=1):
    """
    Perturb the parameters with random vector z.
    Input: 
    - random_seed: random seed for MeZO in-place perturbation (if it's None, we will use self.zo_random_seed)
    - scaling_factor: theta = theta + scaling_factor * z * eps
    """

    # Set the random seed to ensure that we sample the same z for perturbation/update
    torch.manual_seed(random_seed if random_seed is not None else self.zo_random_seed)
    
    for name, param in self.named_parameters_to_optim:
        z = torch.normal(mean=0, std=1, size=param.data.size(), device=param.data.device, dtype=param.data.dtype)
        param.data = param.data + scaling_factor * z * self.args.zo_eps

 

 

3. Results

MeZO는 prompt-based fine-tuning 방식에서만 잘 작동한다. Prompt는 Making pre-trained Language Models Better Few-shot Learners의 방법을 차용하였다.

 

 

Medium-sized masked LMs (RoBERTa-large, 350M), large autoregressive LMs (OPT-13B, 30B, 66B)에 대해 실험을 진행했다. 

 

[RoBERTa]

 

 

[OPT]

 

 

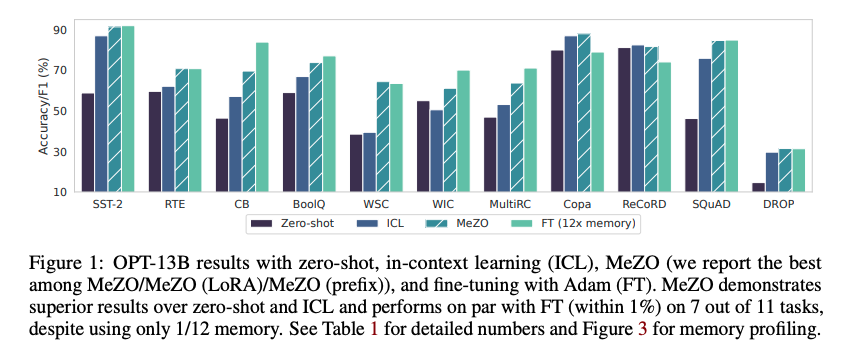
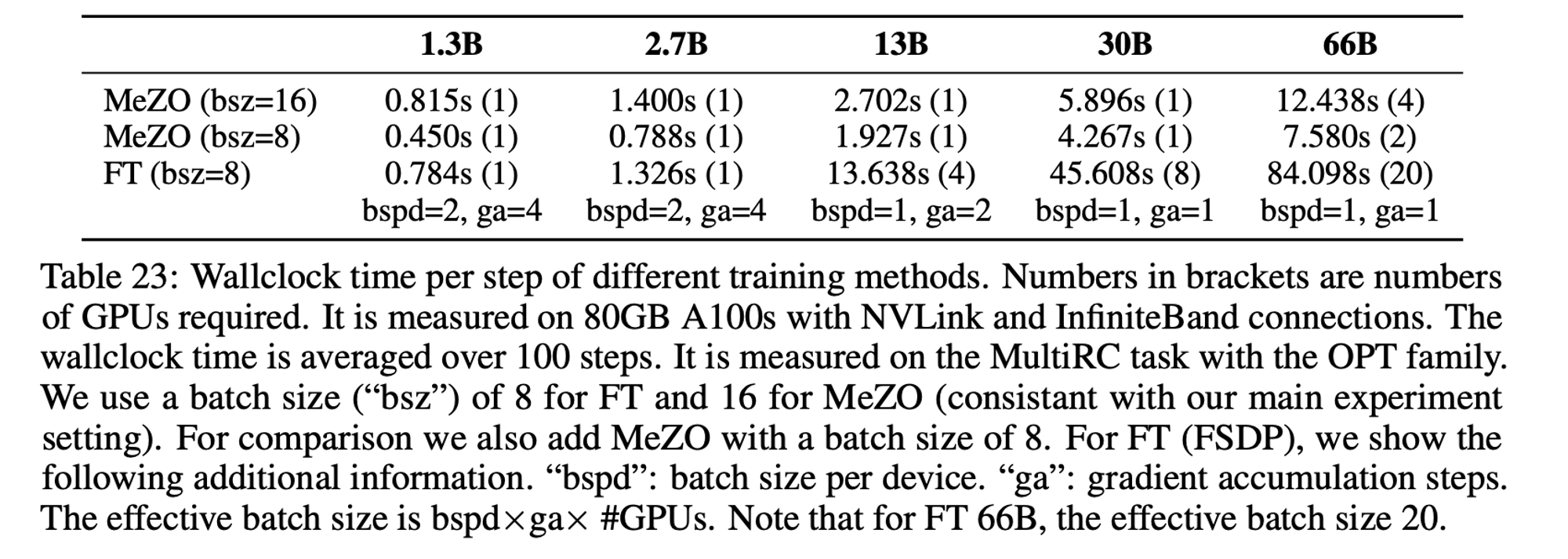
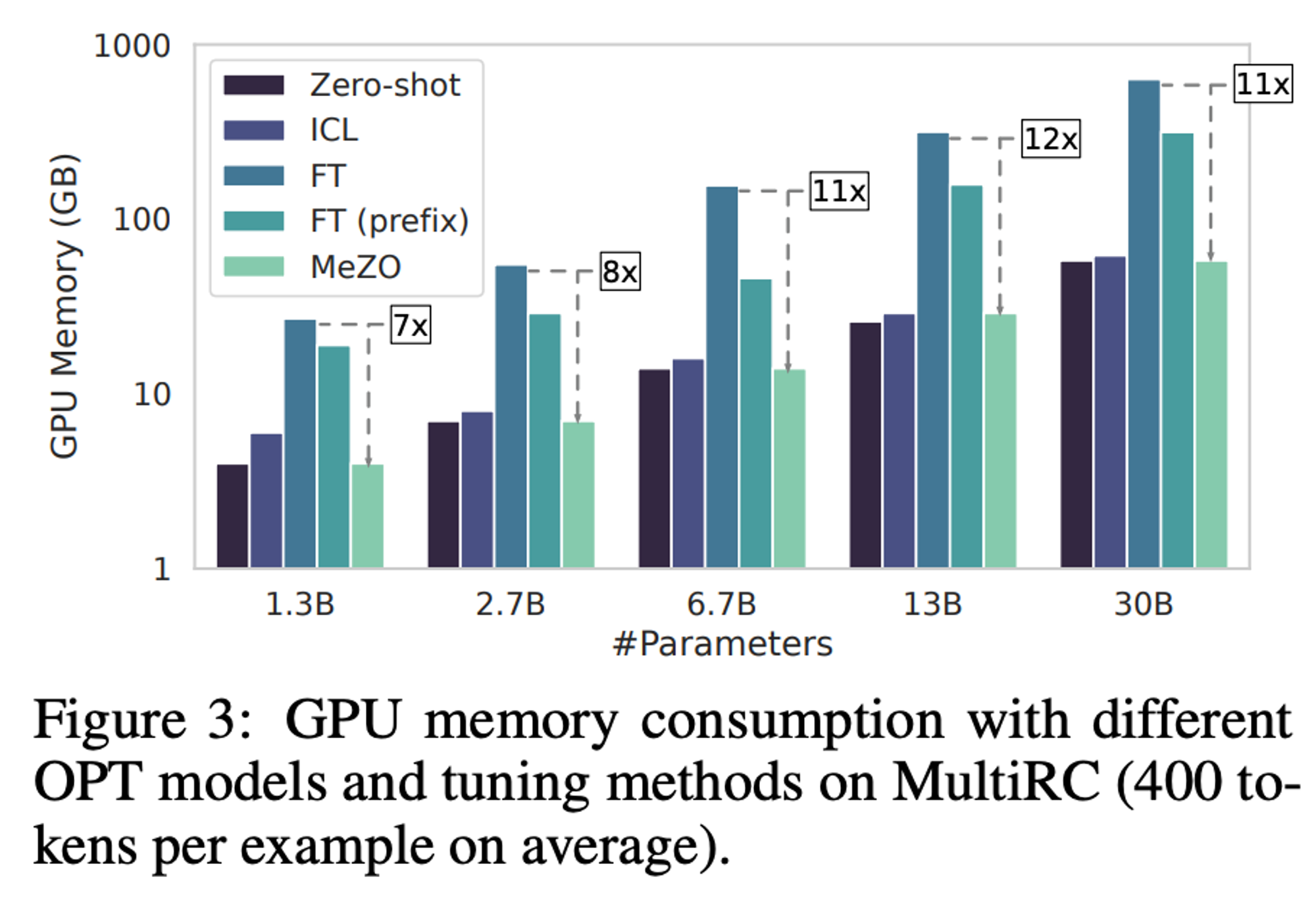
Fine-Tuning의 1/12 메모리, 절반의 시간만 사용하고도 1% 내의 성능을 낸다. (OPT-13B 모델)

 

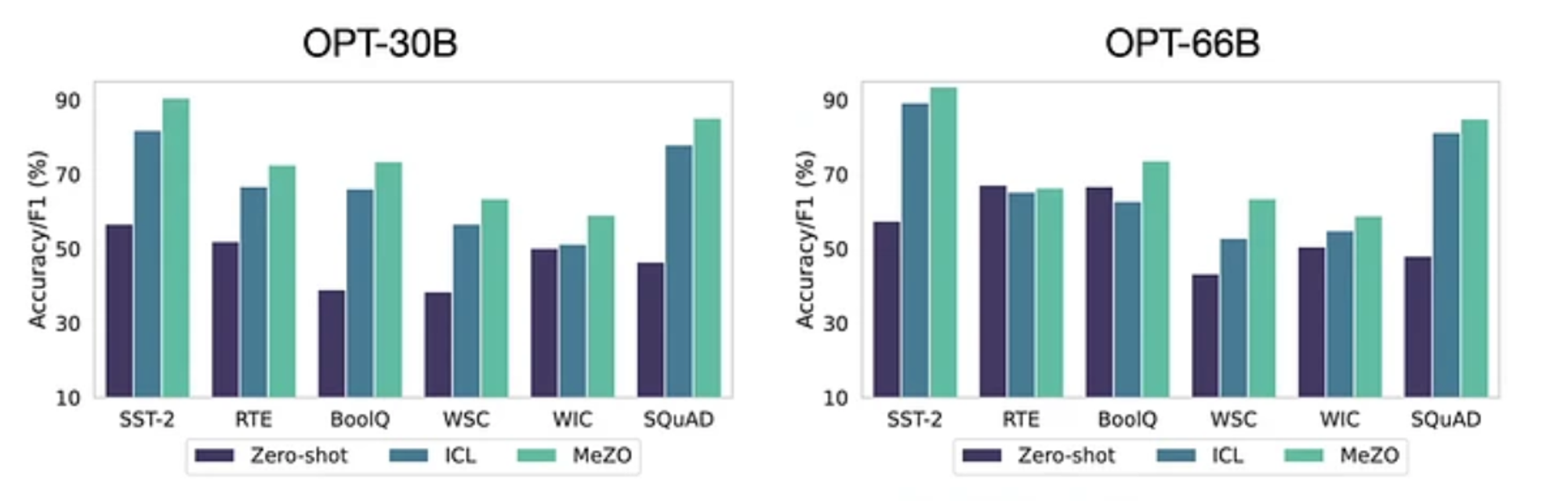
더 큰 모델에서도 잘 동작하는데,  Zero-shot과 ICL보다 훨씬 상회하는 성능을 보이는것을 알 수 있다. (FT 결과가 없는것은 큰 모델에선 FT보다 성능이 많이 떨어져서일까?)

 

 

[시간 효율성과 메모리 효율성]

 

 

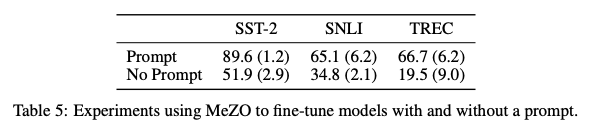
[Non-differentiable objectives]

 

Non-differentiable objective (accuracy, F1 score 등)에 대해서도 optimize할 수 있다. 따라서, human preference 등을 이용한 parameter update도 기대할 수 있다.